Quotient Groups

Ifis a normal subgroup ofthen the coset spacewith the binary operation

for allbelonging tois a group. The identity element of this group is the trivial coset

Let G be a group and let H be a subgroup of G. The following statements are equivalent:

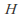1. is a normal subgroup of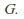

2. For all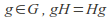(The left and right cosets are identical)

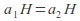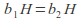3. Coset multiplication is well-defined that is ifandthen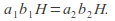Once this is established the rule for multiplication of cosets 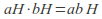follows.

Proof

Ifis normal inand andthenso

Supposefor allSupposeThen

Suppose coset multiplication is well defined. Letsoand sois normal in

Now the main result: Ifis a normal subgroup ofthe set of cosetsbecomes a group under coset multiplication.

Proof

For associativity, note that

and

Hence,is the identity for coset multiplication.

Finallysoforand every coset (element of the sethas an inverse henceis a group, called the quotient group ofby