Splitting Fields

The quadratic equationdoes not factorise. This means that it has no fractional roots of the formwhere a and b are whole numbers. In fact it has no real roots because the discriminant

The set of fractions, or rationals, is a field, labelledhas no rational roots.

In fact the roots are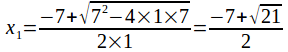and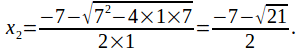

is rational butis not. We cannot express the roots of the polynomial in terms of the fieldbut if we addto the fieldwe can express the roots in terms of the extended field, written

is called an splitting field of the field

Consider the quintic equationThis equation factorises intoThe first factor has rootandabove and the second has rootsandWe can't express the roots of this polynomial in terms of rational fractions or even in terms of the rational fractions andbut we can express the roots in terms of rational fractions,andThis field is writtenand includes all expressions of the formor where

We can always extendto include the roots of a polynomial in this way. We can find a splitting field for any polynomial.