The First Isomorphism Theorem
Let
and
be groups, and let
be a homomorphism. Then:
-
The kernel of
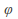is a normal subgroup of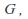
-
The image of
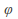is a subgroup of
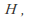and -
The image of
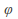is isomorphic to the quotient group
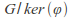whose elements are
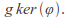The identity in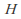is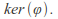
In particular, ifis surjective thenis isomorphic to
In fact given any normal subgroup
we can define a homomorphism
such that 
is surjective (onto) by construction, and well defined since
Example:
Let
is a normal subgroup of
and
The kernel of
is the set of elements of g that are sent byto the identity
Labelling
bywe can write
and