Derivatioin of the Continuity Equation

A conservation law is the statement that a given quantity can be neither created  nor destroyed but may merely move. That leads to the statement :

The total rate of outflow from some region must equal the rate of decrease of that  quantity located within that region.

Suppose we have a cylindrical surface, such that gas can flow in and out through the ends but not through the sides.

Supposedenotes the density of a gas at timeforThus at  any timethe total mass of gas present in the regionis given by

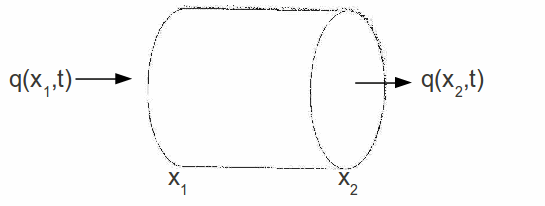
Let us denote byandthe mass inflow/outflow of the gas at the endsandrespectively.

The rate of change of mass of gas in the region betweenandis given by

andare held fixed and since

By adding these we obtain

In higher dimensions, we obtain

This is the continuity equation. The rate of flow of mass of gas out of a surface element of areaisWe can write the continuity equation asThe region of integrationcan be chosen arbitrarily, and since any continuous function with integral zero over an arbitrary region must be the zero function, hence