The sum of a sequence is said to converge if
There are two very useful theorems for deciding whether or not the sum of a sequence converges.
The Ratio Test
If there exists
such that
for
then
converges. The test says nothing about sequences such that
where
means 
from below.
Proof:
Suppose first that
for all
Hence
Example:
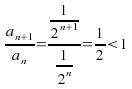thereforeconverges.
The Comparison Test
We can prove convergence of divergence for some sequences by comparing the sequence with a 'standard' sequence, the sum of which which either converges or diverges.
For example suppose
and
then
The proof is obvious.
Standard convergent sequences include
Standard divergent sequences include
Example:
which is a standard convergent sequence thereforeconverges.