Sums, products, differences and quotients of series converge in the obvious way.
Theorem
If
converges to
and
converges to
then
converges to
Proof: Choose
There is a positive integer
such that if
then
and a positive integer
such that if
then
Let
then if
and 
then
Hence
converges to
Theorem
If
converges toandconverges to
then
converges to
Proof:
Choose
Since
there is a positive integer
such that if
then
a positive integersuch that ifthenand a positive integer
such that if
thenLet
then if
and
so take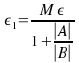
then
Theorem
Ifconverges to
andconverges to
then
converges to
Proof: ChooseThere is a positive integersuch that ifthenand a positive integer
such that if
thenLet
then ifand then
Henceconverges to
Theorem
Ifconverges toandconverges tothen
converges to
Proof: ChooseSinceconverges, it is bounded so there exists
such that
for all
Let
There is a positive integersuch that ifthen
and a positive integersuch that ifthen
Letthen ifand then
Henceconverges to