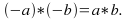The basic properties of the set of real numbers![]() are given below.
are given below.
-
Closure: For all real numbers
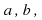 the sum
the sum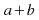 and the product
and the product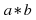 are real numbers.
are real numbers. -
Associative laws: For all real numbers
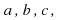
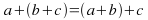 and
and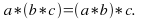
-
Commutative laws: For all real numbers
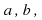
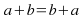 and
and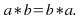
-
Distributive laws: For all real numbers
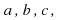
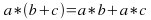 and
and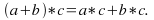
-
Identity elements: There are real numbers
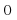 and
and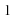 such that for all real numbers
such that for all real numbers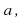
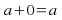 and
and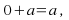 and
and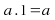 and
and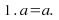
-
Inverse elements: For each real number
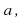 the equations
the equations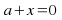 and
and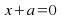
have solutions
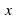 in the set of real numbers, called the additive inverse of
in the set of real numbers, called the additive inverse of 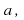 denoted by
denoted by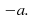
For each nonzero real number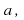 the equations
the equations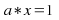 and
and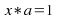
have solutions
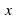 in the set of real numbers, called the multiplicative inverse of
in the set of real numbers, called the multiplicative inverse of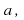 denoted by
denoted by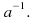
Here are some additional properties of real numbers![]() which can be proved from the properties listed above.
which can be proved from the properties listed above.
-
If
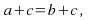 then
then-html-m2c667033.gif)
-
If
-html-m1c6d8502.gif) and
and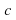 is nonzero, then
is nonzero, then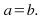
-
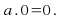
-
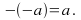
-