Suppose we have a function![]() sends any point
sends any point![]() in the plane to another point
in the plane to another point![]() We can define smooth curves that pass through
We can define smooth curves that pass through![]() The function
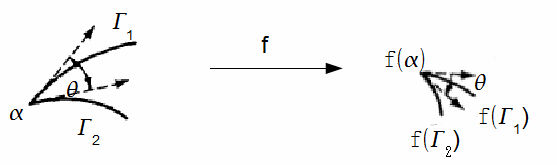
The function![]() is conformal if the angle between any two paths through
is conformal if the angle between any two paths through![]() is unchanged by the transformation. This is shown below. The angle between
is unchanged by the transformation. This is shown below. The angle between![]() and
and![]() is the same as the angle between
is the same as the angle between![]() and
and![]()
A function is conformal if it is conformal on its domain. In fact, any analytic function is conformal at any point![]() for which
for which![]()
Proof:![]() higher order terms.
higher order terms.
![]() higher order terms.
higher order terms.
Subtract these two to give![]() higher order terms. The tangent vectors
higher order terms. The tangent vectors![]() and
and![]() are both rotated by
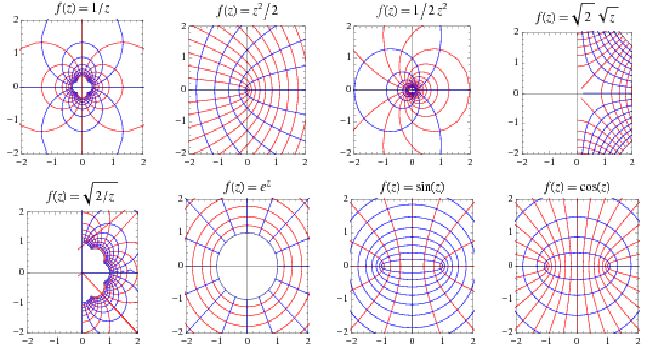
are both rotated by![]() but the angle between them is unchanged. In general of course entire regions are mapped. Some examples are shown below. The grid lines in the plane are transformed onto the curves. Since the angle between any tow grid lines is a right angle, so is the angle between any two curves.
but the angle between them is unchanged. In general of course entire regions are mapped. Some examples are shown below. The grid lines in the plane are transformed onto the curves. Since the angle between any tow grid lines is a right angle, so is the angle between any two curves.