A Mobius transformation is any rational function of the form![]() where
where![]() and
and![]() satisfy
satisfy![]()
Properties:
Every Mobius transformation is conformal – preserves angles – and analytic on![]()
Every Mobius transformation is either a linear function or a quotient of linear functions. If
![]() then
then![]() and
and![]()
Every Mobius transformation![]() may be extended to
may be extended to![]() so that if
so that if![]() then
then![]() and
and![]() The extended function is labelled
The extended function is labelled![]() Extended Mobius transformations map
Extended Mobius transformations map![]() one to one onto
one to one onto![]() and generalized circles – circles and lines – onto generalized circles.
and generalized circles – circles and lines – onto generalized circles.
If![]() then
then![]() where
where![]()
The set of extended Mobius transformations has the following group properties:
-
Closure: If
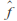 and
and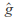 are extended Mobius transformations then so is
are extended Mobius transformations then so is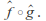
-
Identity: The identity function in
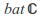 is an extended Mobius transformation.
is an extended Mobius transformation. -
Associativity: If
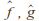 and
and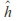 are extended Mobius transformations then
are extended Mobius transformations then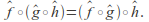
An extended Mobius transformation![]() has at least one fixed point
has at least one fixed point![]() such that
such that![]()
An extended Mobius transformation is defined by it's effect on three distinct points.
Given three distinct points![]() in
in![]() and any other three distinct points
and any other three distinct points![]() in
in ![]() there is a unique extended Mobius transformation that sends
there is a unique extended Mobius transformation that sends![]() to
to![]() to
to![]() to
to ![]() In particular if
In particular if![]() are
are![]() respectively then
respectively then![]()
If![]() are generalized circles then there is an extended Mobius transformation that maps
are generalized circles then there is an extended Mobius transformation that maps![]() to
to![]()
