Convergence does not have a single definition. We may say that a function converges to a limit function
but it is not enough to say
We must be more precise.
A sequence of functions
converges pointwise to a limit function
on a set
if, for each
We relate this definition to the ordinary
definition which states:
is continuous at a point
if for each
there exists
such that if
then 
Pointwise convergence implies that we must make
dependent on
For example,
converges to the zero function
on
To prove thatis continuous at
we must findsuch thatimplies
with r<1.
Take
so that
implies that if
then
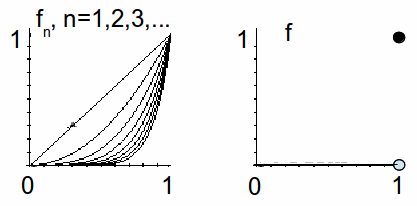
Though useful, pointwise convergence does not give a type of convergence strong enough for many purposes. In fact for the case above, if we extend the domain slightly to include 1, the sequence
does not even converge to a continuous function, since
if
but
if
