If![]() with
with![]() then the number and nature of the fixed points and the intersection of the keep set
then the number and nature of the fixed points and the intersection of the keep set![]() with the real axis depends on the value of
with the real axis depends on the value of![]()
![]() has
has
-
No fixed real points if
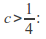
-
A single fixed point if
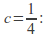
-
Two real fixed points
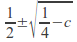 if
if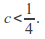
If![]() then the fixed points are complex so
then the fixed points are complex so![]() The coefficients of
The coefficients of![]() are real so the roots are complex conjugates and since there is no intersection with the real axis, the keep set is not connected. Further, the intersection of the keep set with the imaginary axis is also zero, since
are real so the roots are complex conjugates and since there is no intersection with the real axis, the keep set is not connected. Further, the intersection of the keep set with the imaginary axis is also zero, since![]()
If![]() then
then![]() has either 1 or 2 real fixed points so
has either 1 or 2 real fixed points so![]() is non – empty. In fact, if
is non – empty. In fact, if![]() then
then![]() is the interval
is the interval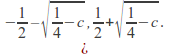
If![]() then
then![]() consists of the closed interval
consists of the closed interval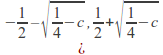 from which a sequence of disjoint, non – empty, open subintervals have been removed. In particular,
from which a sequence of disjoint, non – empty, open subintervals have been removed. In particular,![]() Furthermore, there is no intersection of
Furthermore, there is no intersection of![]() with the imaginary axis since
with the imaginary axis since![]() so
so![]() is outside the interval above and
is outside the interval above and![]() is not in the keep set.
is not in the keep set.
