Regions

A region in the complex plane is a non - empty, open, connected set. The following are all regions.

Any open disc

Any open half plane

The complementof any closed disc

Any open annulus

The setitself

Any open rectangle, triangle, pentagon or similar shape

Any open, connected set with a finite number of points excluded

Proving the last of these is a set is quite easy.

Theorem

Ifis a region andthenis also a region.

Proof

Since R is a region it contains an open disc centred onsois non – empty. Alsois closed insois open andis open as the intersection of two open sets.

Suppose thatSinceandis a region, we can joinand by a pathinand the path also lies inif

If howeverlies onthen choose an open disc(possible since R is a region) and modifyinside this disc to avoid

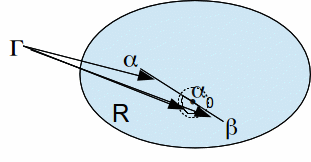
The resulting path joinsandinsois connected andis a region.

We can apply this region recursively to exclude any finite number of points