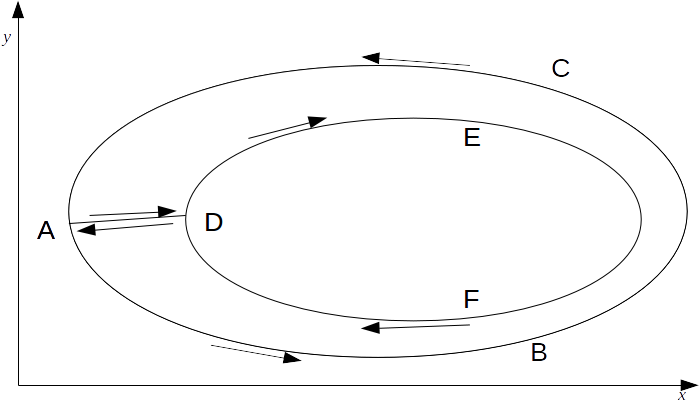
\[\begin{equation} \begin{aligned} \int \int_R ( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} dx \: dy &= \oint_{ABCDEF} P dx + Q dy \\ &= \int_{ABCA} P dx + Q dy + \int_{AD} P dx + Q dy + \oint_{DEFD} P dx + Q dy + \oint_{DA} P dx + Q dy \\ &= \int_{ABCA} P dx + Q dy + \oint_{DEFD} P dx + Q dy \\ &= \oint_{C} P dx + Q dy \end{aligned} \end{equation}\]
Where
\[C\]
is the boundary \[ABC \cup DEF\]
of the region \[R\]
