Rouche's Theorem

Suppose

1. A function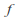is analytic on a simply connected region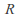

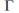2. is a simple closed contour in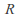

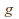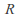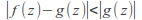3. is analytic onandfor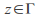

Thenhas the same number of zeros asinsidecounted according to their multiplicity.

Proof: By 2 above, ifthenlies inside the open disc with centreand radius

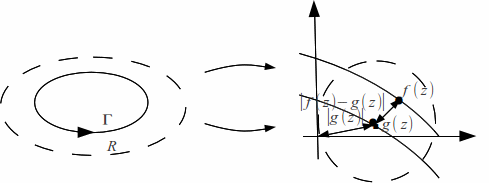
Sincecannot pass on the opposite side of the origin asso andcircle the origin the same number of times and)

Example: Takeandand letbe the circletraversed anticlockwise.

Thenandonso all the conditions of Rouche's theorem are satisfied andandboth have winding number three about the origin.