The Fundamental Theorem of Algebra is on of the most important theorems in analysis. It states:
If
for
with
then
has at least one zero. It can be used to prove thathas
zeros quite easily.
Proof: Suppose that
for all
Then
is entire It is also bounded since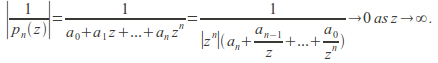
Any bounded entire function is constant by Liouville's Theorem and sois constant. This is a contradition sinceis a polynomial of degree greater than 1 so must have at least one zero.
Suppose
is this zero, then we can write
We can apply the argument repeatedly to
to prove that a polynomial of order
haszeros in
It is important to not that the roots are in general complex. In fact a polynomial may not have any real roots at all. For example if
then the roots are
and
The fundamental theorem only guarantees complex roots, not real roots.