The g Over h Rule for Evaluating Residues

Theorem

Letwhere the functionsandare analytic at the pointand then

Proof:

In order to prove the theorem we first need to show that an if an analytic functionhas a singularity atthenproviding this limit exists.

To do this letIfthenhas a removable singularity atIf then f has a simple pole atand

(Note that we can expandin a Laurent series aboutobtaining

so that

then)

Now putthen(since ), then

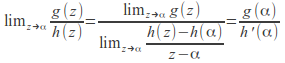
The theorem is proved.

Example: Evaluate the residue ofat

atandatso therule gives