The gamma function extends the factorial function which acts on non – negative integers to complex numbers.
We consider the improper integrals
We can easily find
and can In for n=1,2,3,... by obtaining a reduction formula for
Hence
In general
so for non negative integers the integral exists and takes the values of the factorial function. For general complex numbers the integral is denoted
and is called the Gamma function,
defined as
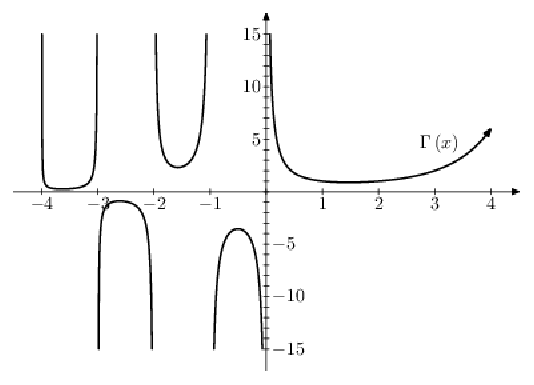
Thefunction is analytic on the half plane
but analytic continuation can extend the domain to the whole complex plane with the exception of the non – positive integers where it has simple poles.
