The uniqueness theorem makes functions well defined. It states
Let
and
be analytic on a region
and suppose thatagrees withon a set
where
has a limit point in
then
on
Ifhas a limit point inthen there are an infinite number of distinct points inwhere
Example: If
and
prove that
Letbe an analytic function on
such that
The set
and has a limit point
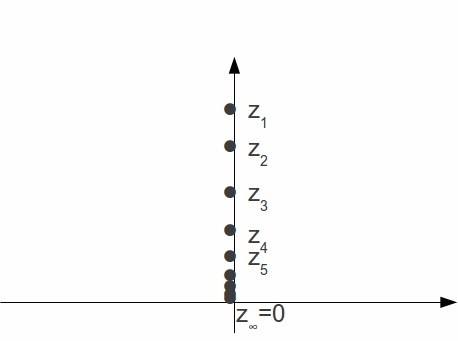
Furthermore if
then
so thaton
All the conditions of the uniqueness theorem are satisfied so that
on