The winding number of a curve
about a point
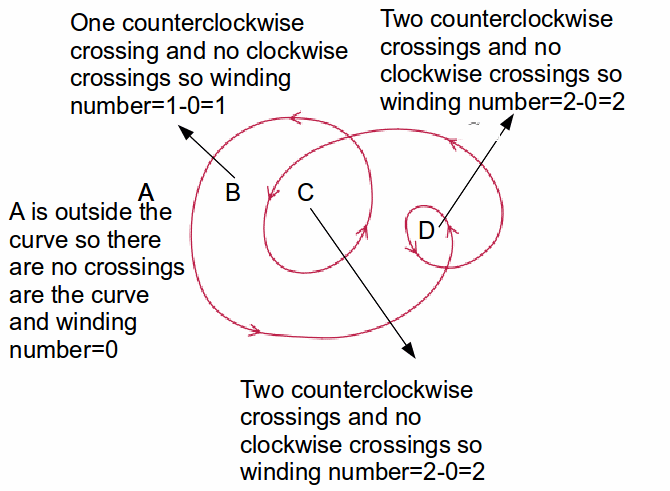
is the number of times the curves makes a complete anticlockwise turns about the point
We can easily label the regions into which a curves divides the complex plane in terms of winding numbers by drawing a line from the point to the part of the complex plane completely outside the curve. The winding number is equal to the number of times the curve passes the line in a counterclockwise direction minus the number of times the curve passes the line in a clockwise direction.
The winding number about a point is also equal to the total increase in argument as the curve
is traversed divided by
and can be found using Cauchy's Integral Formula. For a closed simple curve (with no crossings),
The integral will increase by one for each counterclockwise circuit aroundso is equal to the winding number hence
for an arbitrary closed curve