Variation of Parameters Method of Solving Non Homogeneous Differential Equations

We start from the nonhomogeneous differential equationThe associated homogeneous equationhas fundamental – linearly independent – solutionsandand then the general solution of the associated homogeneous equation iswhereandare constants. The general solution of the original nonhomogeneous equation iswhereis a particular solution of the original nonhomogeneous equation. The method of variation of parameters looks for a particular solutionof the formwhich means finding the functionsandBy substitutinginto the original nonhomogeneous equation we obtain the simultaneous equations

Solving these equations simultaneously gives

and

whereis the determinant of the matrix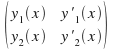 – this determinant is called the Wronskian.

Then

and

Summary

Find two fundamental solutions of the homogeneous equation

Write down the form of the particular solution

Findand

Write down the answer