\[f(x(\]
at a point \[x_0\]
approximates the tangent to the curve \[y=f(x)\]
at \[x_0\]
. It is defined as \[\frac{f(x_0+h)-f(x_0)}{(x_0+h)-x_0}{/jatex.
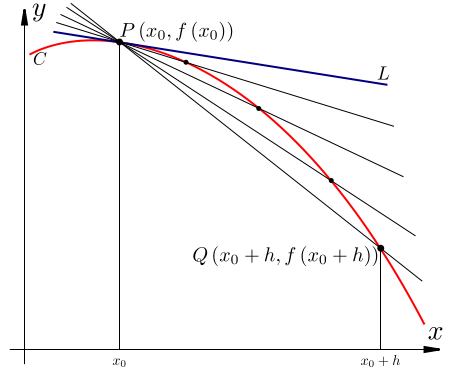If this quotient tends to a limit as {jatex options:inline}h \rightarrow 0\]
we define the derivative of
If this quotient tends to a limit as {jatex options:inline}h \rightarrow 0\]\[f(x)\]
at \[x_0\]
is defined as \[\frac{d(f(x))}{dx}= lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{(x_0+h)-x_0}\]
.