\[R\]
?
\[r\]
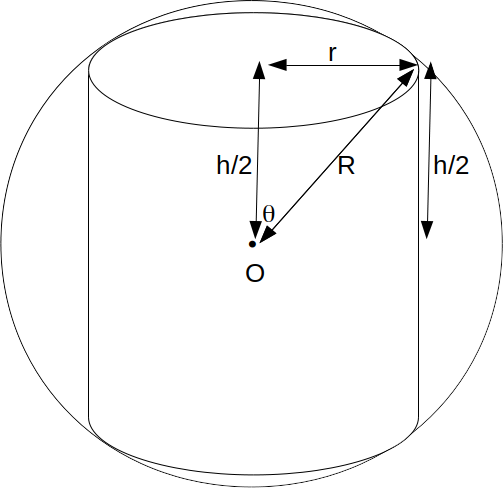
of the cylinder base subtend an angle of \[\theta\]
at the centre of the sphere then \[r=Rsin \theta\]
and if the height of the cylinder is \[h\]
then from the diagram \[h/2=R cos \theta \rightarrow h=2Rcos \theta\]
.The volume of the cylinder is
\[V= \pi r^2h=\pi (R sin \theta )^2 (2R cos \theta )=2R^3 sin^2 \theta cos \theta\]
\[\frac{dV}{d \theta }= 2 \pi R^3 (2 sin \theta cos^2 \theta -sin^3 \theta )\]
Then for maximum volume
\[2 sin \theta cos \theta -sin^3 \theta = sin \theta (2cos^2 \theta -sin^2 \theta )=0 \rightarrow tan^2 \theta =2 \]
\[sin^2 \theta =1- cos^2 \theta = 1- \frac{1}{sec^2 \theta }=1- \frac{1}{1+tan^2 \theta }=1- \frac{1}{1+2}=\frac{2}{3}\]
.
\[cos \theta = \sqrt{1-sin^2 \theta }= \sqrt{1-\frac{2}{3}}= \frac{\sqrt{3}}{3}\]
Then
\[V=2\pi R^3 \frac{2}{3} \frac{1}{\sqrt{3}}= \frac{4 \pi R^3 \sqrt{3}}{9}\]
. 