\[H\]
and base radius \[R\]
, what are the radius of the base and the height of the cylinder that give the maximum volume?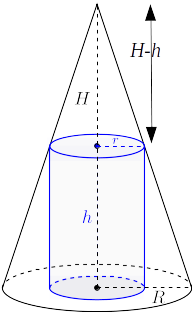
\[\frac{H-h}{}= \frac{r}{R} \rightarrow r= \frac{R(H-h)}{H}\]
.The volume of a cylinder is given by
\[V= \pi r^2h= \pi (\frac{R(H-h)}{H})^2h=\frac{\pi R^2}{H^2}(H^2h-2Hh^2+h^3)\]
\[\frac{dV}{dh}= \frac{\pi R^2}{H^2}(H^2-4Hh+3h^2) \]
The volume is maximum when
\[\frac{dV}{dh}=0 \rightarrow H^2-4Hh+3h^2=0 \rightarrow (H-3h)(H-h)=0\]
.Then
\[h=0 \rightarrow V=0\]
or \[h= \frac{H}{3}\]
and \[r=R \frac{H-h}{H}=R \frac{H-H/3}{H}= \frac{2}{3}R\]
.The maximum volume is
\[V= \pi r^2h= \pi (\frac{2R}{3})^2 \frac{H}{3}= \frac{4 \pi R^2H}{27}\]
. 