The determinant of 2 by 2 matrix can be worked out almost instantly:
![]() ie multiply the diagonal numbers together and subtract them.
ie multiply the diagonal numbers together and subtract them.
The determinant of a 3 by 3 matrix is much more difficult. We have to carry out a process called expanding along a row or a column, In the example below I will expand along a row – the top row.
Example:
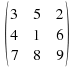
We label the positions in the matrix with +1's and -1's: 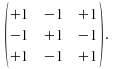 For the first term, 3, cross out the entries in the same row and column as this 3.
For the first term, 3, cross out the entries in the same row and column as this 3.
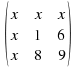
![]()
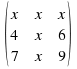 Our second term is
Our second term is ![]()
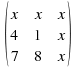 Our third term is
Our third term is ![]()
The determinant is![]()
