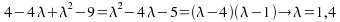Eigenvalues

Given a linear transformation A , a non-zero vector x is defined to be an eigenvector of the transformation if it satisfies the eigenvalue equation

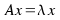(1)

for some scalar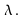In this situation, the scalar 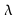is called an "eigenvalue" of A corresponding to the eigenvector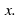In other words the result of multiplying 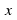b y the matrix is just a scalar multiple 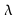of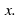

The key equation in this definition is the eigenvalue equation, Most vectorswill not satisfy such an equation: a typical vector changes direction when acted on by A , so that is not a multiple ofThis means that only certain special vectors are eigenvectors, and only certain special scalars are eigenvalues. Of course, if A is a multiple of the unit matrix, then no vector changes direction, and all non-zero vectors are eigenvectors.

The requirement that the eigenvector be non-zero is imposed because the equation holds for every A and everySince the equation is always trivially true, it is not an interesting case. In contrast, an eigenvalue can be zero in a nontrivial way. Each eigenvector is associated with a specific eigenvalue. One eigenvalue can be associated with several or even with an infinite number of eigenvectors.

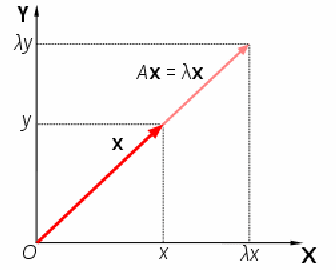
acts to stretch the vector not change its direction, sois an eigenvector of A .

From (1) which we may factorise as hence Det where I is the identity matrix.

We may then form a polynomial equation in 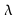and solve it to find the eigenvalues:

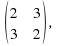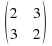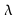
A= A-λI=- 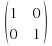which becomes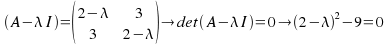

We can simplify, factorise and solve.