\[\mathbf{F}_1=--T_1+T_2\]
The net force on mass 2 is
\[\mathbf{F}_2=--T_2+T_3\]
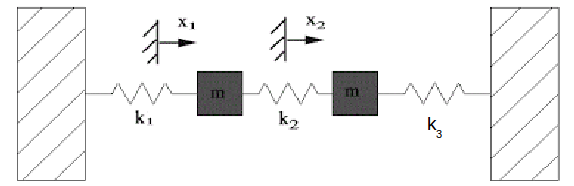
On the diagram above the net increase in length of the central spring is
\[x_2-x_1\]
so the tension in the central spring is \[T_2=k_2(x_2-x_1)\]
.Now use
\[\mathbf{F}_i=m_i \mathbf{a}_i\]
and \[\mathbf{T}_i=-k_- \mathbf{x}_i\]
(note that \[x_3=x_2\]
to get\[m_1 a_1=-k_1x_1+k_2(x_2-x_1)=-2k_1x_1+k_2x_2 \rightarrow a_1=-\frac{2k_1}{m_1}x_1 +\frac{k_2}{m_1} x_2\]
\[m_2 a_2=-k_2(x_2-x_1)-k_3x_2=k_2x_1-(k_2+k_3)x_2 \rightarrow a_1=\frac{k_2}{m_2}x_1 -\frac{k_2+k_3}{m_2}x_2\]
We can write this in matrix form as
\[\begin{pmatrix}a_1\\a_2\end{pmatrix}=\left( \begin{array}{cc} -\frac{2k_1}{m_1} & \frac{k_2}{m_1} \\ \frac{k_2}{m_2} & -\frac{k_2+k_3}{m_2} \end{array} \right) \begin{pmatrix}x_1\\x_2\end{pmatrix}\]
.Suppose that
\[m_1=1, \: m_2=2, \: k_1=1, \: k_2=2, \: k_3=3 \]
. The system becomes\[\begin{pmatrix}a_1\\a_2\end{pmatrix}=\left( \begin{array}{cc} -2 & 2 \\ 1 & -5/2 \end{array} \right) \begin{pmatrix}x_1\\x_2\end{pmatrix}\]
.Find the eigenvalues of the matrix.
\[det( \left( \begin{array}{cc} -2 & 2 \\ 1 & -5/2 \end{array} \right)- \lambda \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right))=\lambda^2+4.5 \lambda^2+3=0\]
.Then
\[\lambda=\frac{-4.5 + \sqrt{8.25}}{2}\]
.Then mass 1 vibrates with a frequency
\[2 \pi \omega_1= 2 \pi \sqrt{- \lambda_1} = 2 \pi \sqrt{\frac{4.5 + \sqrt{8.25}}{2}} \]
, and mass 2 vibrates with a frequency \[2 \pi \omega_2= 2 \pi \sqrt{- \lambda_2} = 2 \pi \sqrt{\frac{4.5 - \sqrt{9.25}}{2}} \]
