\[m_1 , \: m_2\]
respectively. The columns are stiff, of stiffnesses \[k_1, \: k_2\]
respectively. The joints between the columns and the girders are rigid, and vibrations are undamped. When vibrations occur the girders remain horizontal.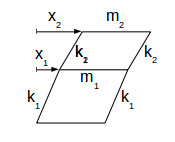
\[x_1 , \: x_2\]
respectively, then applyting Newton's Second Law to each girder gives\[m_1 \ddot{x}_1=-k_1 x_1+k_2(x_2-x_1) \rightarrow \ddot{x}_1=(- \frac{k_1}{m_1}+ \frac{k_2}{m_1}) x_1+ \frac{k_2}{m_1}x_2\]
\[m_2 \ddot{x}_2=-k_2(x_2-x_1) \rightarrow \ddot{x}_2=\frac{k_2}{m_2}x_1- \frac{k_2}{m_2}x_2 \]
We can write this in matrix form as\[ \begin{pmatrix} \ddot{x}_1 \\ \ddot{x}_2 \end{pmatrix} = \left( \begin{array}{cc} - \frac{k_1}{m_1}+ \frac{k_2}{m_1} & \frac{k_2}{m_1} \\ \frac{k_2}{m_2} & - \frac{k_2}{m_2} \end{array} \right) \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\]
The frequencies of vibration of the system are the square roots of the negatives of the eigenvales of the matrix.\[\begin{equation} \begin{aligned} \left| \begin{array}{cc} - \frac{k_1}{m_1}+ \frac{k_2}{m_1} - \lambda & \frac{k_2}{m_1} \\ \frac{k_2}{m_2} & - \frac{k_2}{m_2} - \lambda \end{array} \right| &= \frac{\lambda^2 m_1m_2+ \lambda(m_1-k_1m_2-k_2m_2)+k_1k_2}{m_1m_2} \\ &= \frac{\lambda^2 m_1m_2+ \lambda(m_1-k_1m_2-k_2m_2)+k_1k_2}{m_1m_2}=0 \end{aligned} \end{equation}\]
.If the eigenvalues - the solutions to this quadratic are
\[\lambda_1 \: \lambda_2\]
the the frequencies of vibrtation of the structures are \[\omega_1= \sqrt{-\lambda}_1 , \: \omega_2= \sqrt{-\lambda}_2\]
. 