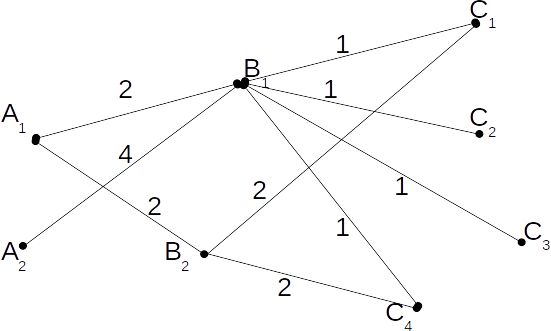
We can represent the information in the diagram in table form,| B1 | B2 | |
| A1 | 2 | 2 |
| A2 | 4 | 0 |
| C1 | C2 | C3 | C4 | |
| B1 | 1 | 1 | 1 | 1 |
| B2 | 2 | 0 | 0 | 2 |
\[T_{AB}=\left( \begin{array}{cc} 2 & 2 \\ 4 & 0 \end{array} \right), \; T_{BC}= \left( \begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 0 & 0 & 2 \end{array} \right)\]
.We can find the number of possible options for flying from A to C.
\[\begin{equation} \begin{aligned} T_{AC} &= T_{AB}T_{BC} \\ &= \left( \begin{array}{cc} 2 & 2 \\ 4 & 0 \end{array} \right) \left( \begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 0 & 0 & 2 \end{array} \right) \\ &= \left( \begin{array}{cccc} 6 & 2 & 2 & 6 \\ 4 & 4 & 4 & 4 \end{array} \right) \end{aligned} \end{equation}\]
.