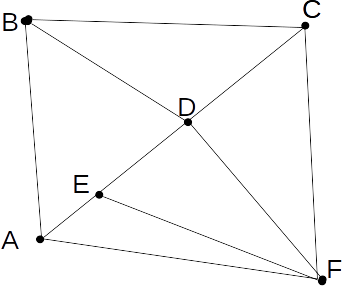
| A | B | C | D | E | F | |
| A | 0 | 1 | 0 | 0 | 1 | 1 |
| B | 1 | 0 | 1 | 1 | 0 | 0 |
| C | 0 | 1 | 0 | 1 | 0 | 1 |
| D | 0 | 1 | 1 | 0 | 1 | 1 |
| E | 1 | 0 | 0 | 1 | 0 | 1 |
| F | 1 | 0 | 1 | 1 | 1 | 0 |
\[M=\left( \begin{array}{cccccc} 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 & 0 \end{array} \right)\]
.One way to think of this matrix is that the entry
\[a_{ij}\]
gives the number of route with one arc from vertex i to vertex j.\[M^2=\left( \begin{array}{cccccc} 3 & 0 & 2 & 3 & 1 & 1 \\ 0 & 3 & 1 & 1 & 2 & 3 \\ 2 & 1 & 3 & 2 & 2 1 \\ 3 & 1 & 2 & 4 & 1 & 2 \\ 1 & 2 & 2 & 1 & 3 & 2 \\ 1 & 3 & 1 & 2 & 2 & 4 \end{array} \right)\]
.The entry
\[a_{ij}\]
gives the number of route with two arcs from vertex i to vertex j.In general the element
\[a+{ij}\]
of \[M^n\]
will give the number of routes with n arcs from vertex i to vertex j. 