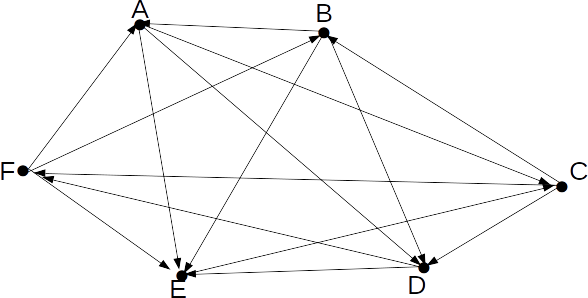
| Winner\Loser | A | B | C | D | E | F |
| A | 0 | 0 | 1 | 1 | 1 | 0 |
| B | 1 | 0 | 0 | 1 | 1 | 0 |
| C | 0 | 1 | 0 | 1 | 0 | 1 |
| D | 0 | 0 | 0 | 0 | 1 | 1 |
| E | 0 | 0 | 1 | 0 | 0 | 0 |
| F | 1 | 1 | 0 | 0 | 1 | 0 |
The matrix of the table is:
\[M= \left( \begin{array}{cccccc} 0 & 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0\end{array} \right)\]
\[M^2= \left( \begin{array}{cccccc} 0 & 1 & 1 & 1 & 1 & 2 \\ 0 & 0 & 2 & 1 & 2 & 1 \\ 2 & 1 & 0 & 1 & 3 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 2 & 2 & 2 & 0\end{array} \right)\]
represents the two step wins (team 1 loses to team 2, but beat team 3 who also beat team 2). We can use \[M+M^2= \left( \begin{array}{cccccc} 0 & 1 & 2 & 2 & 2 & 2 \\ 1 & 0 & 2 & 2 & 3 & 1 \\ 2 & 2 & 0 & 2 & 3 & 2 \\ 1 & 1 & 1 & 0 & 2 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 2 & 1 & 2 & 2 & 3 & 0\end{array} \right)\]
.Adding up the rows gives 9 for team A, 9 for team B,11 for team C, 6 for team D, 4 for team E and 10 for team F. Team C wins, and the teams are ranked C, F, A=B, D,E.
