Closure of the Reciprocal Sequence in a Metric Space

Theorem

Letbe the space of real numbers in the metric spacewith the absolute value metricand let

The closure ofisand the closure of any subsetofis a closed subset of

Proof

LetThe closure ofwrittenis defined aswhere

Since

For each

Henceand

Chooseandthenhence

To prove the closure of any subsetofis a closed subset ofsupposeis not closed thenis not open and there is an elementsuch that for every

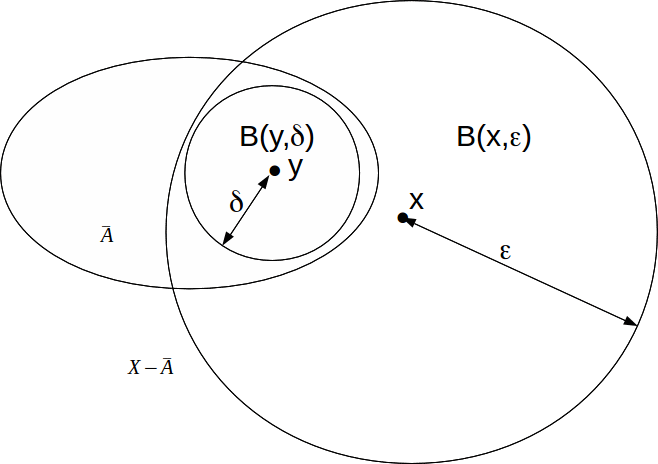
Choose

Sinceis open there existssuch that

Sincethensoexists such that

Hence forthere existssuch that Hence contradicting