Non-Euclidean geometry is the geoemtry of 'curved space' as opposed to Euclidean or 'flat' geometry in which Euclid's postulates all hold. The postulates may be dropped one by one giving rise to hyperbolic geometry, elliptic geometry, spherical geometry, descriptive geometry, differential geometry, geometric algebra, and multidimensional geometry. These geometries deal with generalisations of surfaces and curves in space rather than the lines and planes and curves in Euclidean geometry. The first five postulates of Euclidean geometry will be listed in order to better understand the changes that are made to make it non-Euclidean.
1.) A unique straight line can be drawn from any point to any point.
2.) A finite straight line can be produced continuously in a straight line.
3.) A circle may be described completely by centre and radius.
4.) All right angles are equal.
5.) If a transversal falls on two lines in such a way that the interior angles on one side of the transversal are less than two right angles, then the lines meet on the side on which the angles are less than two right angles.
A consistent logical system for which one of these postulates is modified in an essential way is a non - Euclidean geometry. Although there are different types of Non-Euclidean geometry which do not use all of the postulates or make alterations of one or more of the postulates of Euclidean geometry, hyperbolic and elliptic are usually most closely associated with the term Non-Euclidean Geometry. Many models of the Universe use these two geometries.
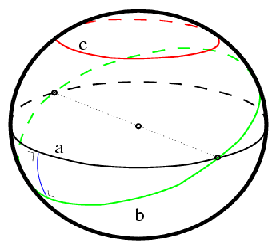
Hyperbolic geometry is based on changing Euclid's parallel (5 th ) postulate, which may also be stated : one and only one parallel to a given line goes through a given point not on the line, while elliptic geometry results from a modification of postulate 2, which allows for lines of infinite length, which are denied in Elliptic geometry, where only finite lines are assumed. Elliptic Geometry includes the geometry of the surface of a sphere. Any line drawn on a sphere meets itself, so has finite length as shown below.