The five postulates of Euclidean geometry are
-
That between any two points a unique straight line can be drawn.
-
A line can be extended without limit on length.
-
A circle is completely described by it's centre and radius.
-
All right angles are equal.
-
The parallel postulate: "That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles." This is shown below.
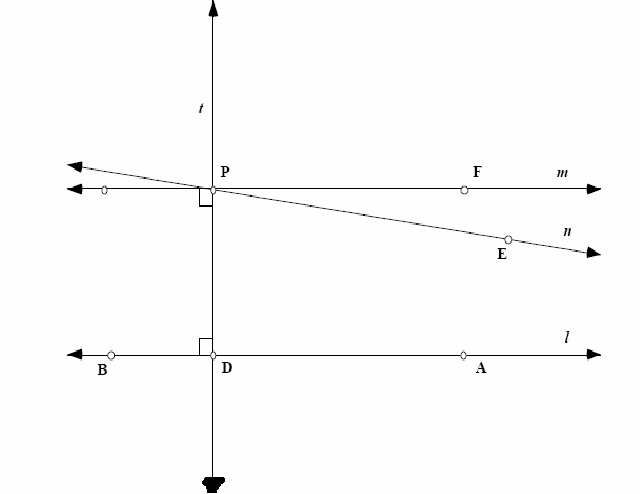
Other geometries than Euclidean geometry is possible, in which the postulates are abandoned or modified. These are the 'non – Euclidean geometries.'
