The Error Term For Polynomial Approximations

Interpolation may used to approximate either a known function or a set of data for an unknown function. It is not possible to evaluate the error for an unknown function.

If(i.e.is a functiontimes differentiable inwith continuous derivatives) andis the polynomial that interpolatesthenthere existsthat depends onsuch that

Proof: This result is trivially true forsince both sides are zero.

Fordefine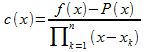so that

Define the function

which satisfiesforand

hasdistinct roots in

By Rolle's theorem, there must be at least one root ofbetween two successive roots ofSohas at leastdistinct roots in

Apply Rolle's theorem to derivatives of increasing order successively, to show thatmust have at least one root inCall this pointso that

The nth derivative ofisbutis a polynomial of degreeso

Letso that

Hence

Using this we can obtain bounds on the accuracy of Lagrange interpolation, provided we can bound the nth derivative,Since the error term involvesLagrange interpolation is exact for polynomials of degreeat most.

Example: Estimate the error for f(x)= sin(3x) interpolated for the points

at

So, the error in the approximation tois

The actual error is

However, the functioncannot be approximated accurately by an interpolation

polynomial, using equidistant points on the intervalAlthoughis differentiable, its derivatives grow asforeven sodoes not converge to 0 whileincreases (since interval width > 1).