Instead of using the derivative of a function
to find the next iterate in the search for the root of
as in the Newton-Raphson method, we may to use the last two iterates,
to find an estimate for
By definition,
We put
to obtain
We then use this estimate in
to obtain
The Newton Raphson method needs an initial guess for the root,
The secant method needs two initial guesses,
and
Example: Solve
starting with
and
|
|
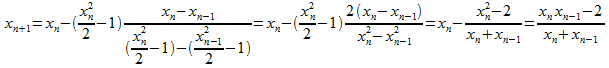
0 |
1 |
2 |
3 |
4 |
|
|
1.000000 |
1.500000 |
1.400000 |
1.413793 |
1.414216 |
|
|
0.414214 |
0.085786 |
0.014214 |
0.000442 |
0.000002 |
For this example, the secant method requires one more iteration than Newton's method to approximate
with the same accuracy 
The method is slightly slower than the Newton Raphson method, but it does not require the evaluation of a derivative. It does need two initial points but these do not have to straddle the root.