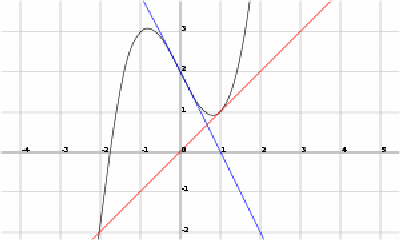
The Newton – Raphson method offers a useful method of finding the roots of functions.
We start from the Taylor series for a function
The first two terms on the right give us the equation of the tangent at
This tangent line intersects the
axis at
so
Rearrangement of this gives
and we can generalise this to give
Iteration gives better approximations to the root
as shown below.
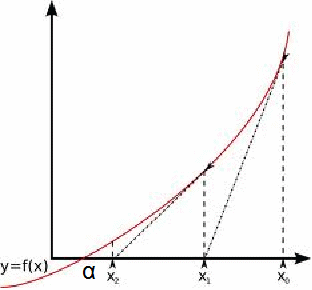
The method is not infallible. The method may not converge to the desired root or diverge from a required root, especially if
is not chosen properly or the gradient is changing rapidly, or if one of the
is such that
is not defined eg when finding the root close to zero of a function with a square root or log.
