Fixed Point Theorem

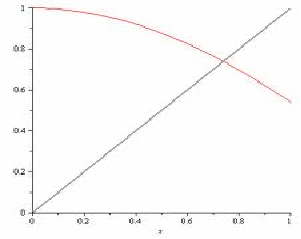
Theorem

Ifis a continuous function fromintothe there exists at least onesuch that

Proof: Suppose thatis a function fromintoSuppose thatand Thenandso by the intermediate value theorem, there existssuch thatHence for thisandhas a fixed point in

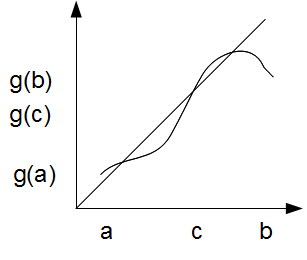
It is important to have the codomain is a subset of the domain. For example fordefined onthe codomain isand no point is fixed. There is of course no solution to

Example:defined onwe havefor some