Proof that Every Infinite Set Contains a Countable Subset

This theorem can be proved using the axiom of choice.

Supposeis an inifite set and letbe the power set of(the set of all subsets of). Define the choice function

For each non empty subsetofBy the Axiom of Choice, such a function exists.

Define

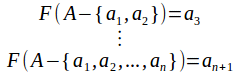
The setis infinite so for

Sinceis a choice functionfor

Hence all theare distinct and the setis a countable or denumerable subset of

The setis infinite because the setis infinite.