If an ordinal number is added to two other ordinal numbers, the order of magnitude of the sum is preserved.
Suppose
and
with
and
The set
is order isomorphic to a subset of
Call this subset
hence a function
exists.
For the sets
and
with
If
we can write 
If
we can write 
or
If
we can write
Then
where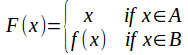
is an order isomorphism from
onto a proper subset of
of
therefore
Also, if
then
Conversely suppose ordinal numbers exist such thatand
When
then either
or
Supposethen
which is a contraction. This rule is called left cancellation. Right cancellation is not true for ordinal numbers.