The Axiom of Choice

Definition: Axiom of Choice. Letbe a collection of nonempty sets. Then we can choose a element from each setso that there exists a function(called a choice function) defined onwith the property that, for each set

Initially controversial, it is now a basic assumption used in many areas of maths. It is independent of the other axioms of set theory. Thus there are no contradictions in choosing to reject it and choosing another instead. The axiom can be stated in many equivalent ways. For example:

• The cardinality of any of two sets is less than or equal to the cardinality of the other. one set has cardinality less than or equal to that of the other. This implies there exists a bijection from one set to a subset of the other.

• Any vector space over a field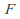has a basis -- a maximal linearly independent subset -- over that field.

• Any product of compact topological spaces is compact.

• The axiom of choice is equivalent to the well-ordering principle.

Examples of choice functions

• If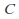is the collection of all nonempty subsets of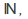then 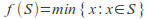is one possible choice function.

• If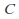is the collection of all bounded intervals of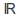we can let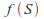be the midpoint of the interval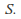

• No choice function has ever been found when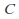is the collection of all nonempty subsets of the real numbers, and it may be that non exists.