Let
be the
plane as a subset of
with the Euclidean topology. Let
be the sphere of radius 1 with centre at
Thenis a compactification of
Let
be the line passing through the point
on the sphere
Take any point
in the plane and draw a line through
and
This line will intersect the sphere at a point
We can define a function
from the plane to the sphere in this way.
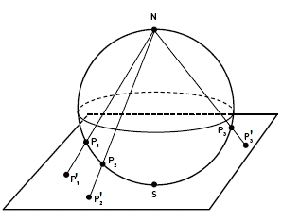
is one to one and onto
and bothand
are continuous. Henceis a homeomorphism from the plane to the subset
of
is not compact whileis compact, and the setis dense in
so thatis a compactification of