Definition of a Topological Space

A topological space is a set together witha collection of subsets ofsatisfying the following axioms:

1. The empty set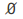and the complete set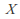are in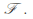

2. The union of any collection of sets in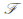is also in

3. The intersection of any finite collection of sets in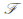is also in

The collectionis called a topology onThe elements ofare called points, though they can be a range of objects. A topological space in which the points are functions is called a function space. The sets inare called the open sets, and their complements inare called closed sets. A subset ofmay be neither closed nor open, either closed or open, or both.

Examples:

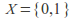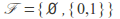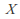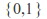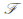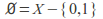1. with the collection consisting of only the two subsets ofrequired by the axioms form a topology, the indiscrete topology. The indiscrete topology always contains only two sets in this way. By definitionandare open inbutand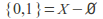so both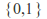andare both open and closed.

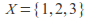2. and collection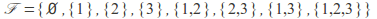of all subsets of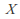form another topology, called the discrete topology. In general a set with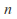points gives rise to a discrete topology with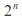sets.

3. The set consisting of all open sets of the form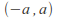is a topology on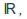In this topology,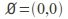and

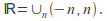
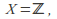4. the set of integers, and collection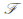equal to all finite subsets of the integers plus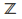itself is not a topology, because (for example) the union of all finite sets not containing zero is infinite but is not all of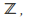and so is not in

A given set may give rise to many topologies, depending on the open sets defined. Every set gives rise to the discrete and indiscrete topologies.especially gives rise to many, quite apart from the standard topology generated by the set of open intervals. For example, the setstogether withand form a topology onas do the setstogether withand 9