Proof of Existence of Lebesgue Number for Open Cover of a Compact Metric Space

Theorem

Ifis a compact metric space andis an open cover ofthen there issuch thatfor some %alpha for any

That is, a numberexists such that the- neighbourhoodof any pointis a subset of at least one

The numberis called the Lebesgue number of the cover.

Proof

Sinceis a cover ofeachbelongs to at least one

Eachis open, hence for eachexists such thatfor some

The collection of sets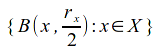is an open cover ofand sinceis compact, a finite subcover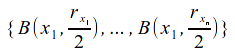exists.

The Lebesgue number is defined as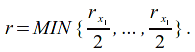

Letthen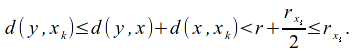

Hencefor some