Proof That a Continuous Image of a Sequentially Compact Set is Sequentially Compact

Theorem

A continuous image of a sequentially compact set is sequentially compact.

Proof

Letbe a continuous function and letbe a sequentially compact subset of

Letbe a sequence inthen there exists a sequence insuch that

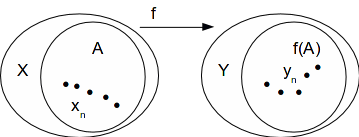
Since A is sequentially compactcontains a subsequencewhich converges to a point

Thenconverges tohenceis sequentially compact.