Proof That a Continuous, Open Function From a Locally Compact Space Onto a Space Produces A Locally Compact Space

Theorem

Ifis a continuous,, open function from a locally compact spaceonto a spacethenis also locally compact.

Proof

A functionis said to be open if, for any open subsetis open in

Letand letbe a neighbourhood ofFor some

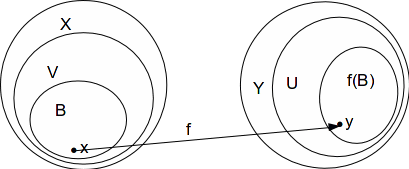
Sinceis continuous, an open setexists such thatand

Sinceis locally compact, there is a compact setsuch that

Then

Sinceis open,is open. Sinceis compact andis continuous,is compact. Henceis locally compact.