Proof That a Contracting Mapping on a Complete Metric Space Has One Fixed Point

Theorem

Ifis a contracting mapping on a complete metric spacethen there exists one and only onesuch that

Proof

LetDefine

so that

Sinceis a contracting mapping,for some

Hence

but

Hence

Since

Hence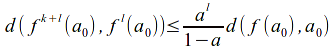

Takeand define

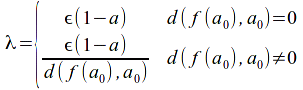
Sinceexists such that

Fo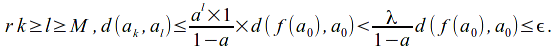

Thusis a Cauchy sequence and sinceis complete,

is continuous hence

is unique since supposethen

so thatand