Theorem
If
is a subset of a second countable space
then overy open cover ofis reducible to a finite cover.
Proof
Let
be a countable base for
and let
be an open cover ofso that
For each
exists such that
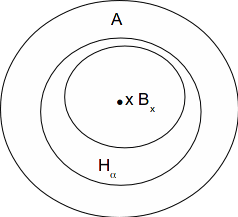
Thus
The family of sets
is a subset of
hence hence it is countable so
where
is a subset of
For each
we can choose
such that
Hence
and
is a countable subcover of