Theorem
The property of being regular is inherited, so that a subset of aregular space is regular.
Proof
Let
bea regular space and let
bea subspace.
Let
andlet
bea
closedsubset of
suchthat
and
where
isthe closure ofin
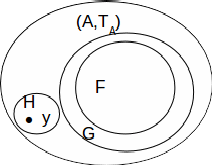
Sinceisregular, open sets
and
existsuch that
But
and
are
opensubsets of
because
and
Sets
and
aredisjoint because
Also, since
and
isalso regular.