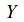The Alexandroff or one Point Compactification of a T2 - Space

Letbe a T2 space. Ifis compact then we can define the Alexandroff compactification ofto beitself.

Now supposeis not compact. Letbe any point not belonging to

Definethen the topology onis such thatis open inor ifthen is a compact subset of

The Alexandroff, or one - point compactification ofis defined as the setwith the topology defined above.

The pointis called the ideal point.

It can be shown that

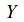1. is compact

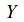2. is a topological space

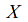3. is dense in