\[I_1, \: I_2, \: I_3\]
respectively, are on a shaft with torsional stiffness \[C\]
. What are the natural frequencies of oscillations of the flywheels?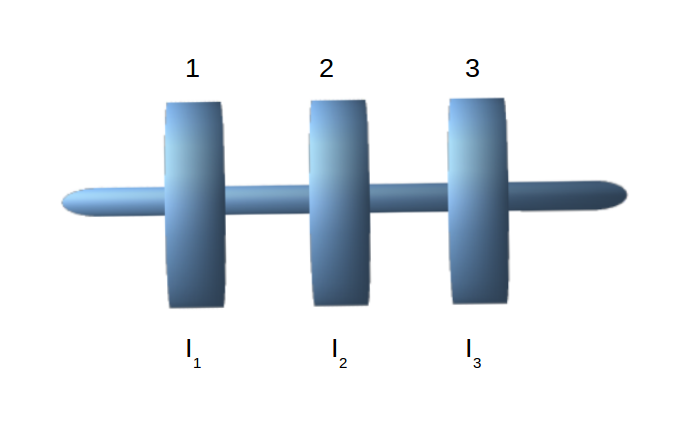
\[\theta_1, \: \theta_2, \: \theta_3\]
respectively. The rotation of each flywheel exer_1ts a torque on the shaft and hence on the other flywheels.For flywheel 1
\[\Gamma_1 = I_1 \ddot{\theta}_1= C(\theta_2 - \theta_1)\]
For flywheel 2
\[\Gamma_1 = I_2 \ddot{\theta}_2= C(\theta_1 - \theta_2)+C(\theta_3 - \theta_2)=C(\theta_1-2 \theta_2+ \theta_3)\]
For flywheel 3
\[\Gamma_3 = I_3 \ddot{\theta}_3= C(\theta_2 - \theta_3)\]
Divevide the equations by
\[I_1, \: I_2, \: I_3\]
resctively and write in matrix form as\[\]
\[\begin{pmatrix} \ddot{\theta}_1 \\ \ddot{\theta}_2 \\ \ddot{\theta}_3 \end{pmatrix} \left( \begin{array}{ccc} - \frac{C}{\Gamma_1} & \frac{C}{\Gamma_1} & 0 \\ \frac{C}{\Gamma_2} & -2 \frac{C}{\Gamma_2} & \frac{C}{\Gamma_2} \\ 0 & \frac{C}{\Gamma_3} & - \frac{C}{\Gamma_3} \end{array} \right) \begin{pmatrix}\theta_1 \\ \theta_2 \\ \theta_3 \end{pmatrix}\]
The amgular frequencies of the vibration are the square roots of the negative eigenvalues,
\[\omega_i = \sqrt{- \lambda_i}\]
and the frequenceies are then \[f_= =2 \pi \sqrt{- \lambda_i}\]
. 